Các phương pháp tính phổ biến được trình bày theo sơ đồ dưới đây

Các phương pháp tính phổ biến được trình bày theo sơ đồ dưới đây.

1. Phương pháp Thống kê Cân bằng

Phương pháp Thống kê Cân bằng (Balance Statistics) đơn giản nhất về lạm phát kỳ vọng (hay nhận thức), được đề xuất bởi Anderson (1952), là sự khác biệt giữa tỉ lệ phần trăm của những người được khảo sát kỳ vọng (hay nhận thức) về giá tăng và giá giảm. Trong trường hợp các câu hỏi khảo sát phân bậc có thể được biểu thị như sau:

BSe = \(A_e^1 + A_e^2 + A_e^3 − Ce\)
BSp = \(A_p^1 + A_p^2 + A_p^3 − Cp\)
  • BSe = Thống kê cân bằng lạm phát kỳ vọng
  • BSp = Thống kê cân bằng lạm phát nhận thức
  • \(A_e^1 (A_p^1)\) biểu thị tỷ lệ phần trăm người trả lời kỳ vọng giá sẽ tăng nhanh hơn [nhận thấy rằng mức giá cao hơn nhiều so với 12 tháng trước);
  • \(A_e^2 (A_p^2)\) biểu thị tỷ lệ phần trăm người trả lời kỳ vọng giá sẽ tăng cùng với tốc độ hiện tại [nhận thấy rằng mức giá cao hơn vừa phải);
  • \(A_e^3 (A_p^3)\) biểu thị tỷ lệ phần trăm người trả lời kỳ vọng giá sẽ tăng với tốc độ chậm hơn [nhận thấy rằng mức giá cao hơn một chút);
  • \(C_e (C_p)\) biểu thị tỷ lệ phần trăm người trả lời kỳ vọng giá giảm [nhận thấy rằng mức giá thấp hơn 12 tháng trước).

Một phiên bản khác của phương pháp này, cũng được đề xuất bởi Anderson (1952), tính toán dựa trên sự khác biệt giữa tỷ lệ phần trăm người được hỏi kỳ vọng (nhận thức) sự tăng giá, sự ổn định hoặc giảm giá:

BSe = \(A_e^1 + A_e^2 + A_e^3− Be – Ce\)
BSp = \(A_p^1 + A_p^2 + A_p^3 − Bp –Cp\)

Trong đó Be (Bp) là tỷ lệ phần trăm người trả lời mong đợi giá sẽ giữ ở mức hiện tại (nhận thấy rằng giá là như nhau).

Ngoài ra, cũng có phương pháp Thống kê cân bằng chú trọng đến các mức độ khác nhau của các thay đổi giá cả kỳ vọng (nhận thức thể hiện trong các cuộc khảo sát đa phân, có trọng số khác nhau cho từng loại phản hồi. Theo đó BSe 3 (BSp 3) có trọng số là 1 (theo Del Giovange, Sabbatini 2004; ECB 2002 – 2007), các tỷ lệ phần trăm của từng phản hồi có tỷ lệ lần lượt là 1, ½, 0, -1/2, và -1:

BSe = \(A_e^1 +1/2A_e^2 – 1/2Be −Ce\)
BSp = \(A_p^1 + 1/2A_p^2− 1/2Bp −Cp\)

Trong một thống kê khác, người ta sử dụng các trọng số tương ứng lần lượt là: 3, 2, 1, 0 và -1

BSe = \(3A_e^1+ 2A_e^2 + A_e^3– Ce\)
BSp = \(3A_p^1 + 2A_p^2 + A_p^3 –Cp\)

Sự phân bổ giống nhau của các câu trả lời cho câu hỏi khảo sát có thể phản ánh các giá trị khác nhau đáng kể của lạm phát kỳ vọng (nhận thức) trong các nền kinh tế hoặc các khoảng thời gian được đặc trưng bởi lạm phát cao hay thấp. Diễn giải kết quả của phương pháp Thống kê cân bằng là đo lường lạm phát kỳ vọng (nhận thức) trung bình và áp đặt các điều kiện nhất định lên các giá trị hàm ý của mức giá cả kỳ vọng (cảm nhận) theo từng tỷ lệ phần trăm của người trả lời.

Giả sử rằng π biểu thị sự thay đổi giá trung bình mà tỷ lệ phần trăm thứ i của những người được hỏi cảm nhận được. Trong trường hợp này, lạm phát nhận thức trung bình có thể được tính theo cách sau:

\(π p = A_p^1π p + A_p^2π p + A_p^3π p + Bpπ p + Cpπ p\)

Nếu cho một Thống kê cân bằng \(BS_k^p,k={1,2,3,4} \)đo lường mức độ nhận thức sự thay đổi giá cả (ví dụ như tỷ lệ của lạm phát nhận thức trung bình):

Trong đó α biểu thị trọng số của tỷ lệ phần trăm thứ i của người trả lời được giả định trong khi tính toán Thống kê cân bằng \(BS_k^p\) và m là hằng số. Từ phương trình trên, có thể dễ dàng nhận thấy rằng các trọng số được sử dụng để tính toán thống kê cân bằng áp đạt các mối quan hệ nhất định đối với các giá trị hàm ý của lạm phát nhận thức trong từng tỷ lệ phần trăm của người trả lời, chẳng hạn:

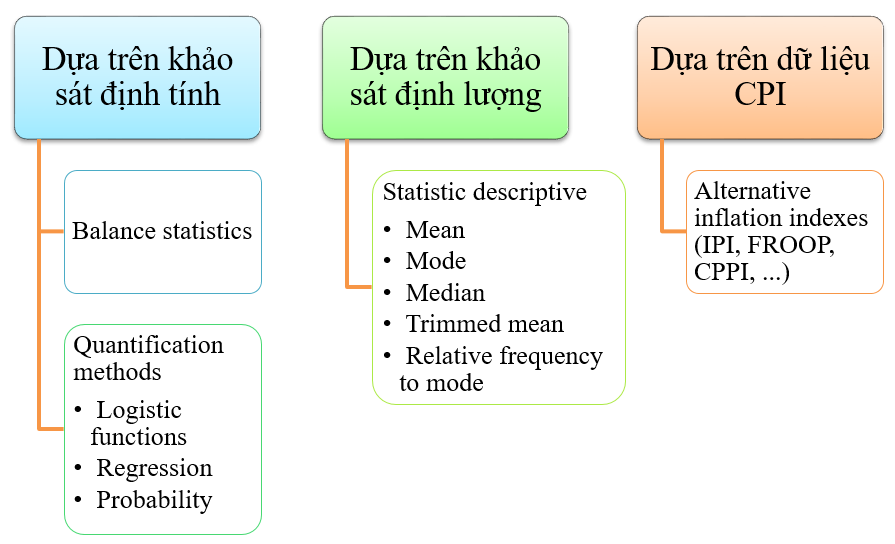
2. Phương pháp Thống kê Mô tả

Phương pháp thứ hai dùng trong báo cáo là phương pháp thống kê mô tả, tập trung vào hai giá trị chính là: trung bình (mean) và trung vị (median), một trong những giá trị của thước đo hướng tâm (measure of central tendency).

Thứ nhất, trị số trung bình số học của một tập hợp các giá trị đo lường (còn được gọi là trung bình số học – arithmetic mean, hay đơn giản là trung bình – mean) bằng tổng số các giá trị đo lường này chia cho số lượng giá trị đo lường. Nếu chúng ta biểu thị n số lượng phải được tính tổng số là x1, x2, …, xn thì tổng số của chúng là:  Khi đó trung bình mẫu và trung bình tổng thể được tính như sau:

  • Trung bình mẫu: 
  • Trung bình tổng thể: 

Thứ hai, trung vị m của một tập hợp n các giá trị đo lường x1, x2, …, xn là giá trị của x mà nằm ở giữa khi các giá trị đo lường này được xếp theo thứ tự từ nhỏ đến lớn dần. Quy tắc tính toán số trung vị như sau:

  • Nếu số n giá trị đo lường là lẻ, thì số trung vị sẽ là giá trị đo lường có thứ hạn bằng (n + 1)/2.
  • Nếu số n giá trị đo lường là chẵn, thì số trung vị được chọn là giá trị của x nằm ở điểm giữa hai giá trị đo lường ở khoảng giữa –  đó là ở điểm giữa giá trị đo lường có thứ hạn bằng n/2 và giá trị đo lường có thứ hạn (n/2) + 1.

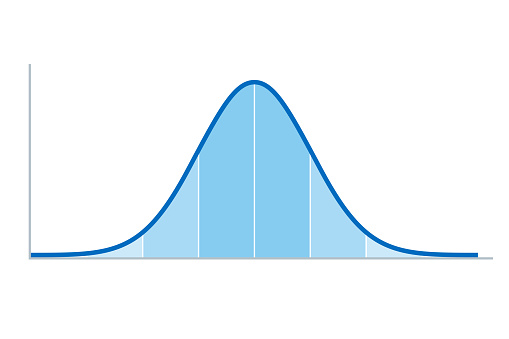
Mặc dù cả trung bình lẫn trung vị đều là hai thước đo tốt đối với trung tâm của một phân phối các giá trị đo lường, nhưng trung vị lại kém nhạy cảm hơn với những giá trị thái cực (hay cực trị). Ví dụ, nếu một phân phối đối xứng qua trung bình của nó như Hình a thì số trung bình và trung vị bằng nhau. Ngược lại, nếu một phân phối không đối xứng và có những quan sát thái cực nằm ở đuôi bên phải (hoặc trái) như Hình b, số trung bình sẽ dịch chuyển sang phải (hoặc trái) bởi vì những giá trị thái cực lớn ở đuôi trên của phân phối này làm tăng tổng số của các giá trị đo lường (Manikandan, 2011).

Do vậy, có một cách khác để tính giá trị trung bình là trung bình cộng gia quyền
hay trung bình cộng có trọng số. Đó là già trị trung bình cộng thể hiện sự quan
trọng của các phần tử (hay giá trị quan sát) trong tập hợp số đó. Mỗi giá trị
quan sát được gắn với một trọng số. Trong đó:

  • Quyền số: Đại lượng có quan hệ với các giá trị của dãy số, nói cách khác đây là
    thành phần tham gia vào quá trình tính toán.
  • Trọng số: Đại lượng phản ánh độ tin cậy hoặc dùng để so sánh tầm quan trọng của các thông tin/đại lượng khác phục vụ cho việc tính toán.

Công thức để tính trung bình cộng có trọng số:

Trong đó wi­ là trọng số của các phần tử.